
Mathematicians generally agree that beauty does exist in the structural beauty of theorems and proofs, even if most of the time it is largely visible only to mathematicians themselves.
—Enrico Bombieri, “The Ree Group Formula”
I have complex feelings about math, none of which are as complex as math itself. I don’t want to be “innumerate” in a tech world, but retain my teenage wannabe-artist obstinacy. I want to believe I am able to practice my way into competency in a variety of disciplines, but can’t make myself prioritize it in my day to day life. What would I, could I take away from “Concinnitas,” ten plain prints of mathematical expressions?
Luckily, I haven’t quite lost my sense of curiosity. Curiosity is the most important thing to bring to this exhibition at the Krakow Witkin Gallery—and to every art show. But for this particular one, you should also make sure you are willing to spend the time it takes to read an accompanying essay for each piece.
It’s only a small consolation that my engineer husband only recognized one or two of the mathematical expressions featured. The collection of aquatints are the responses from ten mathematicians and physicists prompted to transcribe what they believe to be “the most beautiful mathematical expression.” The traveling portfolio is published by Bob Feldman of Parasol Press and curated by Dan Rockmore, with the prints themselves created by Harlan & Weaver, Inc. “Concinnitas” refers to the balance of number, outline, and position that Renaissance scholar, artist and architect Leon Battista Alberti believed characterize a beautiful work of art. All images and accompanying statements can be found at ConcinnitasProject.org.

These “most beautiful” mathematical expressions are artistically expressed not as interpretative illustrations, as I thought they might be when I first read the description, but in their bare glory. I quickly realized, though, how reductive a more interpretive approach could end up, both the interpreting artist and the mathematicians.
Still, who is the audience for these prints? While being a mathematician and gallery-goer are certainly not mutually exclusive, I’ll go out on a limb and venture that most attendees won’t “get” the pieces in a gallery glance. Without further reading, most may just conclude: math is hard, and this is supposed to be beautiful, but why did I just look at ten facsimiles of elite, condescending equations?
This assessment isn’t entirely fair; even though the portfolio and artist statements are available online, these large prints do have a formidable in-person presence, making humble chalkboard motif stately behind glass. The deep monochrome black sets off the artists’ enlarged scrawl in a way that would be at home in a minimalist dining room, or one of MIT’s more architectural lobbies just across the river.
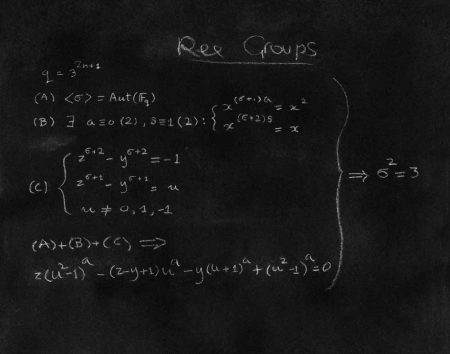
I chafed for an instant when I realized that the mathematicians are named as the artists in this show, since they didn’t create the prints. But it makes sense: in most cases, these expressions are their own masterful discoveries over the course of their careers. Their relatively long statements for each expression touches on their practical application, but also often reflect their own personal journey in using and discovering it. Their admiration inspires, and provides a fascinating context. Plus, it’s their handwriting in each individual print. (The only reason to chafe again is when we realize that all featured artists are men, which Mr. Witkin was quick to point out as unintentional, and his only stalwart reservation about the show.)
Sir Michael Atiyah addressed this artistic sentiment more explicitly than most others for “The Index Theorem,” quoting Karl Weierstrauss in his statement: “It is not possible to be a complete mathematician without having the soul of a poet.” His is perhaps the most enjoyable accompanying essay, imminently scan-able with a few famous quotes peppered in. He acknowledges his collaborators on his chosen equation, as the other artists have as well, with another lovely truism: “Beauty is a human experience and best shared with friends.”
In essence, the accompanying essays turn us into these friends, if not as collaborators, at least as appreciators. The goal here is not for the gallery goer to study up for a quiz, which relieves the pressure enough for us to appreciate the creativity and complexity of these works. The collaborative nature of the exhibition itself is an appropriate testament to that spirit.
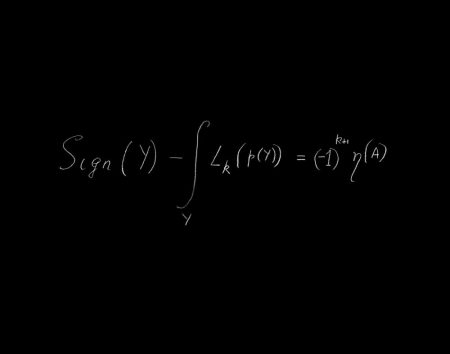
I must also acknowledge this exhibition’s potential to engage others outside of the art community, especially in our notoriously academic city. Expanding an audience in our intellectual city is never a bad choice, and I hope the gallery will see many new attendees in the next month who will consider art and math in a new way.
Case in point: my aforementioned engineer husband. Although he appreciates art, this was one of the few times I’ve seen wax poetic about an exhibition at some length. His reaction was so perfect that I’d be remiss not to let him finish the review:
The beauty of each piece is the conciseness of the expression, and how well it encapsulates a concept—because pure math has very little to do with calculation. It’s distilling a concept into its most distinct form. That lets you use it for other stuff. It’s beautiful in the same way that pointillism or Picasso is. It’s like figuring out a Magic Eye picture, if the hidden image was a Manet. The equation is the album cover to your favorite record. The application is the music, the flash of understanding—your favorite part of your favorite song.